角度を扱う動きや円運動などを行うには、三角関数を利用する。
三角関数と言うと引く諸氏もいるかと思うが、面倒な計算は目の前にあるこんぴーたーにやらせるので、人間としては何と何をもとに何を計算させるかを考えるだけでいい。
理屈を理解出来ればそれほど難解ではない。

三角関数は、sin(サイン)とcos(コサイン)を使う。ASでの命令はMath.sinとMath.cosである。
この２つに角度を与えると、中心点からその角度に１だけ離れた位置の座標を導くことが出来る。
まずはその公式を示す。

//中心点(0,0)から角度の方向に１離れた点を求める X座標 = Math.cos(角度 * Math.PI / 180); Y座標 = Math.sin(角度 * Math.PI / 180);

例によって黒字の部分は意味がわからなくてもよい。
要するに角度だけ入れれば、その角度に１だけ進んだ場所の座標が求められる。

あわせて、こちらを参照。


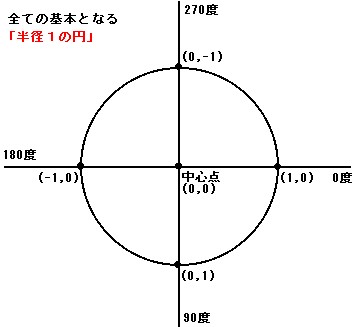この半径１の円が、全ての基本となる。常にこの図を思い浮かべるとよい。

中心点は、円の中心である。ここでは(0,0)であるので、flashで言えば左上の隅ということになる。
円は、中心点を中心とした半径１の円周である。この円のどこの部分でも、中心点からちょうど１だけ離れている。当たり前の事だが再確認。
paraflaでの角度は、真右を０度として、右回りに数える。
角度は、常に0以上360未満の範囲に収まるべきだが、はみ出しても問題は起きないので、自分で修正する必要は特にない。

中心点、角度、距離の３つを与えることで、座標を求めることが出来る。
たとえば円運動をしたければ、中心点と距離を決め、角度を変えていけば実現する。
３つの要素のどれを固定し、どれを変化させるとどうなるのか、図を参考に考えること。

さて、中心点が(0,0)固定、半径が１固定のままでは使えないので、先の公式にそのあたりの汎用性を持たせる。

//中心点から角度の方向に距離だけ離れた点を求める X座標 = 中心点X座標 + Math.cos(角度 * Math.PI / 180) * 距離; Y座標 = 中心点Y座標 + Math.sin(角度 * Math.PI / 180) * 距離;

例えば、スプライトの座標を、(100,50)から60度の方向に40離れた場所にする場合、

_x = 100 + Math.cos(60 * Math.PI / 180) * 40; _y = 50 + Math.sin(60 * Math.PI / 180) * 40;

このように状態変数に計算結果を与えればよい。
X座標とY座標、Math.cosとMath.sinを間違えないこと。

さて話は少し前後し、
当講義でのクリップアクションによるスプライトの移動の方法は、
最初に、位置と１フレームあたりの変化量を決め、毎フレームそのぶんだけ変化させるという方法を解説した。

ここでもう一つの方法である、
最初の位置だけを決め、毎フレーム座標を計算し直すという方法に触れておく。

スプライトをランダムな位置から右方向に、１フレームに５ずつ移動させる例

onClipEvent (load) { start_x = int(Math.random()*100); start_y = int(Math.random()*100); //スタート位置をランダムに決める あとで必要なので開始位置として変数にとっておく _x = start_x; _y = start_y; //最初の位置へ移動 step = 0; //何フレーム経過したかを数える変数 //座標を求めるために必要である } - onClipEvent (enterFrame) { step = step + 1; //stepを1フレームに1ずつ増やしていく _x = start_x + (step * 5); //開始位置とstepをもとに、今いるはずの場所を計算し直して_xに入れる(=移動) }

先の変化量を最初に決める方法では、直線的な変化しか出来ない。
円運動などは全く直線的ではないので、１フレームあたりの変化量が毎回変化するために算出できない。毎フレーム計算し直す手段が必要になる。

まずは最も簡単である円運動から考える。
先の半径１の円を参照。

三角関数で座標を導くために必要なのは、中心点、角度、距離の３つである。
円運動させるには、このうち中心点と距離を固定したまま、角度を変化させればいいことがわかる。

(100,100)を中心とし、半径50の円周上を、１フレームに5度の速さで回る例

onClipEvent (load) { point_x = 100; point_y = 100; //中心点座標 dist = 50; //距離 (distanceの意で…) kakudo = 0; //角度を表す変数 _x = 150; _y = 100; //最初の位置に表示(しなくてもいい) } - onClipEvent (enterFrame) { kakudo = kakudo + 5; //1フレームに5ずつ角度を増やしていく //360以上になっても自動的に修正されるのでそのあたりは考えない _x = point_x + Math.cos(kakudo * Math.PI / 180) * dist; _y = point_y + Math.sin(kakudo * Math.PI / 180) * dist; //三角関数を使って今の座標を計算して_x,_yに入れる(=移動) }

中心点、角度、距離を使って他のこともできる。
中心点、角度を固定し、距離を0から増やしていくと、中心点から任意の角度に進むことになる。
角度をランダムにして複製すれば、中心点から周りにぱーっと広がるような動きが出来る。

(100,100)を中心とし、ランダムな角度に、毎フレーム5の速度で進む(複製スプライト用)

onClipEvent (load) { point_x = 100; point_y = 100; //中心点座標 dist = 0; //最初の距離 kakudo = int(Math.random()*360); //角度をランダムに決める _x = 100; _y = 100; //最初の位置に表示(しなくてもいい) } - onClipEvent (enterFrame) { dist = dist + 5; //1フレームに5ずつ中心点からの距離を増やしていく _x = point_x + Math.cos(kakudo * Math.PI / 180) * dist; _y = point_y + Math.sin(kakudo * Math.PI / 180) * dist; //三角関数を使って今の座標を計算して_x,_yに入れる(=移動) if (_x < 0 || _x > 200 || _y < 0 || _y > 200) { this.removeMovieClip(); } //上下左右いずれかの端から出たら自殺する //「||」は「または」 }

向きを持ったスプライトを、進んでいる方向に合わせて角度を変えるには注意が必要である。
スプライトの角度を決めるには、状態変数 _rotation を使うが、
前述の通り、角度とは真右が0度であり、普通に下を向いているような画像を使うと、0度、つまり右を向くべき時に下を向いているということになる。

それに合わせて角度を計算し直す方法もあるが、もっと単純に右を向いている画像を用意すれば、何も考えずに済む。


角度を変える画像は右向きのものを用意すること

先の３−２のloadハンドラに、青い１行を追加する

kakudo = int(Math.random()*360); //角度をランダムに決める _rotation = kakudo; //スプライトの向きを角度と同じにする

駆け足で三角関数の基本と簡単な応用を解説した。
いくらでも応用が考えられるので、変わった効果を実現させて欲しい。